Python高性能编程
Python高性能编程
目录
[TOC]
理解高性能Python
代码性能分析
1、基准测试
2、代码瓶颈
3、代码剖析
4、性能优化
列表和元组
问题导入:
- 列表和元组的适用情况?
- 查询列表和元组的复杂度?
1、内存结构
当创建一个数组(列表或元组)时,首先必须申请分配一块系统内存(其每一段都将被当成是一个整型大小的指向实际数据的指针)。
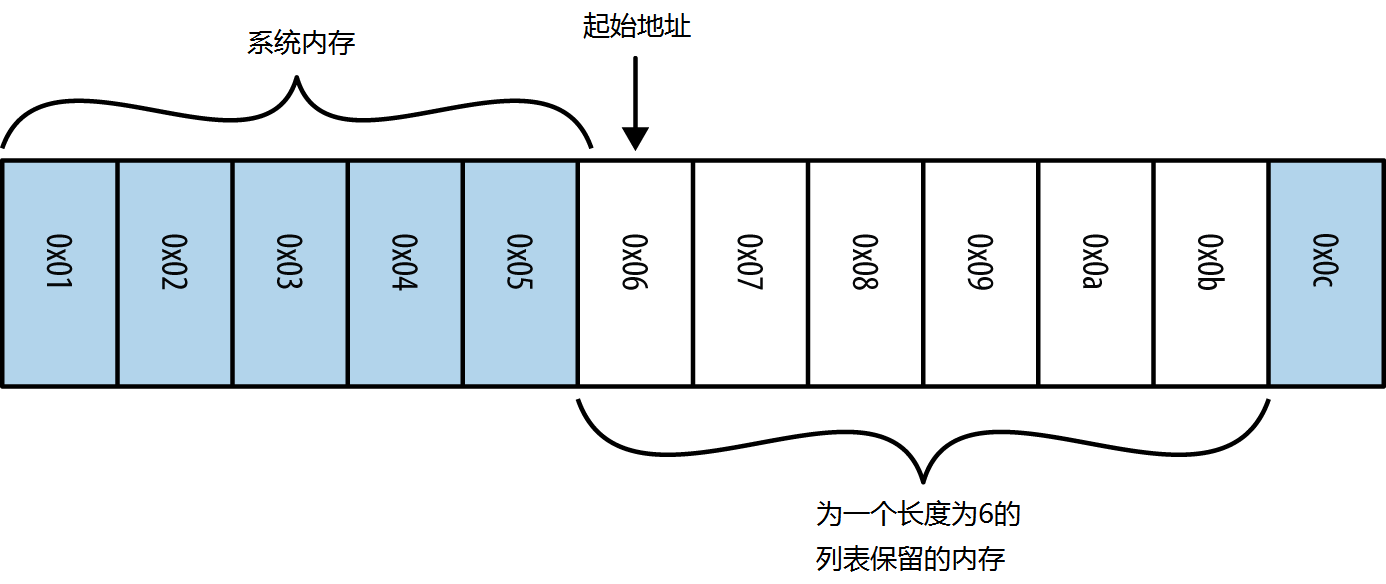
在分配的6 个块中,仅可使用5 个,第一个是列表的长度。
2、高效修改
2-1、列表与双端队列
列表的pop(),append():
| Code | N=10 000(us) | N=20 000(us) | N=30 000(us) | Time |
|---|---|---|---|---|
| List.pop() | 0.50 | 0.59 | 0.58 | O(1) |
| List.pop(0) | 4.20 | 8.36 | 12.09 | O(N) |
| List.append(1) | 0.43 | 0.45 | 0.46 | O(1) |
| List.append(0,1) | 6.20 | 11,97 | 17.41 | O(N) |
使用双端队列在列表首末高效增加删除元素!collections.deque类
双端队列的popleft(),appendleft()
| Code | N=10 000(us) | N=20 000(us) | N=30 000(us) | Time |
|---|---|---|---|---|
| deque.pop() | 0.41 | 0.47 | 0.51 | O(1) |
| deque.popleft() | 0.39 | 0.51 | 0.47 | O(1) |
| deque.append() | 0.42 | 0.48 | 0.50 | O(1) |
| deque.appendleft() | 0.38 | 0.47 | 0.51 | O(1) |
但是,双端队列访问中间元素的时间复杂度为O(N)
| Code | N=10 000(us) | N=20 000(us) | N=30 000(us) | Time |
|---|---|---|---|---|
| deque[0] | 0.37 | 0.41 | 0.45 | O(1) |
| deque[N-1] | 0.37 | 0.42 | 0.43 | O(1) |
| deque[int(N/2)] | 1.14 | 1.71 | 2.48 | O(N) |
2-2、列表的一生:
创建(略)
resize:对于list中所有会改变其大小的操作,都会触发list_resize函数。list_resize接收两个参数,list本身和新的大小;
extends设置的新大小为 m + n;pop设置的新大小为Py_SIZE(self) - 1;append设置的新大小为n+1;首先检查新大小与已分配大小的关系,如果新要求的大小在已分配空间之下并且大于已分配大小的1/2时,则直接改变ob_size,不进行内存调整(1/2 ~ 1);
否则,若新要求的大小大于已分配空间则现有空间不够,若小于已分配空间的一半则需进行内存优化,所以需要进行内存的重新调整(> 1 or < 1/2);
为了避免每新增一个元素就要重新分配内存导致效率的降低,list的内存分配采用跳跃式增长(append);
新分配的空间为 【新大小】 + 【新大小】 * (1/8) + 3(【新大小】< 9)【or 6】;(1.125倍)
这个'跳跃'的高度由newsize的大小决定,容量越大,增长的也越大。
销毁(略)
3、高效搜索
O(1)索引搜索:列表和元组都是以某种内在次序组织的,知道了数据的确定位置,就能以O(1) 时间复杂度查询。
O(n)线性搜索:list.index()的算法。遍历每一个元素并检查,最差O(n)。
1 | # PowerShell |
提升速度的方法:重新组织内存中的数据(哈希散列表,先排序后二分搜索等)。通过散列表可以达到O(1)的复杂度,而对数字排序后二分搜索可以达到O(log n)的复杂度。
3-1、二分搜索(列表已排序)
1 | def binary_search(target, haystack): |
3-2、bisect模块:高度优化二分搜索
可以在保持排序的同时往列表中添加元素,以及一个高度优化过的二分搜索算法函数来查找元素。
| Code | N=10 000(us) | N=20 000(us) | N=30 000(us) | Time |
|---|---|---|---|---|
| List.index(a) | 87.55 | 171.06 | 263.17 | O(N) |
| index_bisect(List, a) | 3.16 | 3.20 | 4.71 | O(log N) |
pass
4、适用情境
!!!元组缓存在Python运行环境,无须请求分配内存,因此访问速度快
1 | # PowerShell |
值得注意的是,列表和元组都可以接受元素有多种类型,但是会增加开销。
4-1、动态数组:列表
列表支持resize操作,可增加数组容量,但是由于跳跃式增长的设置,使用过append()方法的数组大小约为元素大小的1.125倍。
4-2、静态数组:元组
一个使用过append()操作的大小为100000000 的列表实际上占用了112500007 个元素的内存,而保存同样数据的元组始终占用100000000 个元素的内存。这使得元组对于静态数据是一个轻量级且更好的选择。
5、总结
列表可改变,但操作开销大;元组不可变,但保存在缓存里,可以迅速创建。
使用索引O(1)搜索元素,或者使用散列表、二分搜索(bisect模块)获得O(1)、O(log n)的时间复杂度。
注意列表初始化时预分配内存,防止append()等带来的大量开销。
字典与集合
问题导入:
- 字典与集合的适用情况?
- 字典与集合的开销与优化?
- Python命名空间是什么?
1、数据组织结构
如果有一些无序数据但它们可以被唯一的索引对象来引用(任何可以被散列的类型都可以成为索引对象,索引对象通常会是一个字符串)。
graph LR subgraph 关系 A(索引对象)--唯一引用-->B(无序数据) end subgraph 字典 A --> C((KEY)) B --> D((value)) end subgraph Hash H((Key)) -- hash --> I((value)) end subgraph Hashable E(__hash__) E -- + --> F(__eq__) E -- + --> G(__cmp__) end
可散列类型:
hashable(可哈希性)
An object is hashable if it has a hash value which never changes during its lifetime (it needs a
__hash__()method), and can be compared to other objects (it needs an__eq__()or__cmp__()method). Hashable objects which compare equal must have the same hash value.如果一个对象是可散列的,那么在它的生存期内必须不可变(需要一个
__hash__()函数),而且可以和其他对象比较(需要比较方法:__eq__()、__cmp__())。比较值相同的哈希对象一定有相同的哈希值。
字典的Key与Value通过一个哈希散列函数关联,不管规模如何,字典的访问、插入、删除的理论时间复杂度都为O(1),但是极大取决于散列函数计算时间的影响。
集合是没有value的字典。
对具有10 000 个条目以及7 422 个唯一名字的电话簿,集合算法的速度是列表的267 倍!
另外,当电话簿大小增长时,速度的 提升也在增加:
对于一个具有100 000 个条目以及15 574 个唯一名字的电话簿,这 一差距是557 倍
数据来源:《Python高性能编程》[美]Micha Gorelick Ian Ozsvald
2、工作原理
由于字典与集合的高度相似,以下讨论更普遍的字典,其中重点是hash函数及对碰撞的处理。
字典使用哈希函数作为映射,将key转化成列表的索引,搜索时就不需要遍历或二分,因此有O(1)时间复杂度。
2-1、插入与获取
插入元素的位置取决于两个数据:Key的散列值、Key与其他对象的比较。
- 分配一些内存;
插入
- 计算key散列值 --> 掩码;
- 检查是否为空,或含有不一样的value;
graph LR subgraph 检查 F((检查))--无数据-->G(加入key和value) F--有数据-->H(cmp比较键值对) H--key和value相同-->I(终止) H--value不同-->J(覆盖) H--key不同-->K(解决地址冲突) end subgraph 掩码 D[hash值]--&0b111-->E[数组索引] end subgraph 散列 A[KEY]--hash-->B[hash值] B--&掩码-->C[数组索引] end
P.S.掩码是一串二进制数,用于截断另一个数字,例如:使用0b111可获取目标数字的后三位bits表示的数字。(0b后1的个数即为截断的二进制数位数)
1 | 10101010101001010110101 & 0b1111 |
为什么需要掩码?
字典是使用散列函数,通过key计算数组索引的列表,为保证几乎可以是任意数字的散列值落在分配的内存中,使用掩码获取散列值的低位数字。
掩码需要随着内存分配的变化而改变。
地址冲突
Python使用开放寻址法,其中重要的是一个二次搜寻序列,原理见下列网址:
http://svn.python.org/projects/python/trunk/Objects/dictobject.c
为解决地址冲突,Python采用嗅探机制,解决当前冲突,预防未来的冲突。
graph TD A((嗅探))-->B(函数) A-->C(原理) A-->H(二次搜寻序列) B-->D[简单线性函数] C-->G[更新散列值] D-->G C-->E[截取高位比特] C-->F[扰动多个位的比特]
P.S.如果自己设计嗅探函数,需要注意的是,生成新索引的算法需要使新索引均匀地分布在列表中,均匀程度称为“负载因素”,与散列函数的熵有关。
1 | # CPython2.7 |
实例
1 | # 使用上述算法进行地址二次搜寻,解决地址冲突 |
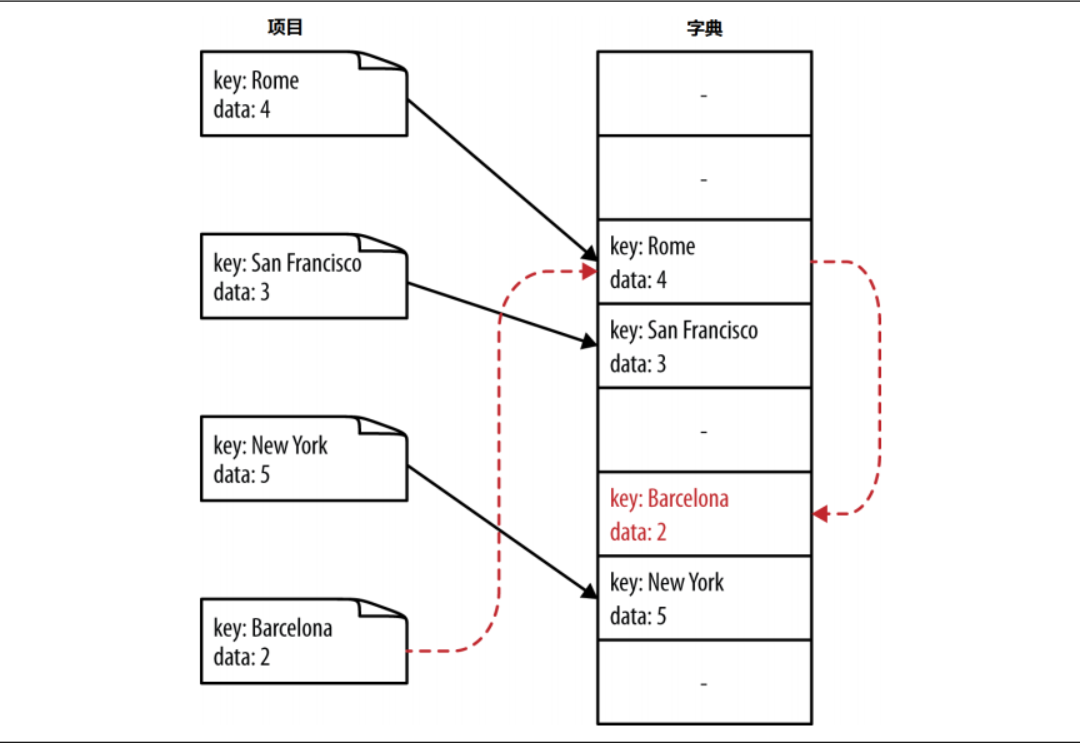
其中,“Barcelona”的初始散列值为2,与“Rome”冲突,经过二次搜寻序列后变为:5
获取
graph LR A[计算散列值]-->B[cmp比较键值对] B--相同-->C[返回找到的键值对] B--不同-->D[嗅探函数] D-->F[生成新索引] F--循环直到找到数据或NULL-->B
P.S.Null被设置为嗅探时散列碰撞的终止值
2-2、删除
一般思路是向对应的内存中写入Null;
但是Null被作为嗅探散列碰撞的终止值;(最后一个搜索过的散列值对应的内存储存Null)
因此选取一个特殊键值对提示:1、该内存可储存数据;2、该内存后还有数据。
标记每个位置,分为“活动桶”、“沉默桶”、“空桶”,删除操作将使用特殊键值对标记该内存为“沉默桶”。同时,针对“活动桶”和“沉默桶”的数量,可以调整该实例分配的内存大小。
2-3、改变大小
.png)
总之:
1、提前指定字典或集合的大小,有助于避免增大散列表时的重新计算索引,提高效率;
2、现有数据数量小于2/3的散列表能较好避免散列碰撞;
3、字典或集合的默认长度为8;
4、大小分配:<50000: x4; >=50000: x2;
3、散列函数和熵
首先,不同的类有不同的散列方式:数字类型(int、float)为基于它们数字的比特值;元组和字符串(tuple、str)为基于它们的内容。!列表不能散列!
对于用户自定义的类:默认__hash__使用id()返回地址,__cmp__比较id()返回的地址。
这就产生了问题:
- 类的单例
- 相同内容,不同实例,如何消除歧义
以下解决第二个问题。
3-1基于内容的自定散列函数
以二维坐标平面点集类为例:
1 | class Points(object): |
由于两个实例不同,使用set或dict,也就是散列表,并不能去除内容重复的元素。
因此,我们需要重载__hash__和__cmp__(__eq__)
1 | class Points(object): |
3-2、设计散列函数
我们定义散列函数的熵: \[ S=-\sum_{i}{p(i)}·log(p(i)) \] p(i) 为散列函数给出散列值为 i 的概率。
当所有 p(i) 相同时,熵最大。
这时散列函数被称为完美散列函数。
4、命名空间的优化
字典的查询速度非常快,但在不必要的情况下使用字典会导致速度的减慢,特别是需要数以百万计的查询。
4-1、Python命名空间
当Python访问某一个变量、函数或模块时,都有一个过程查询它们在哪里。
graph LR A[访问请求]--查询1-->B("locals()") B--查询2-->C("globals()") C--查询3-->D("__builtin__") D--实质-->E("模块的locals()字典")
其中,locals()和globals()为显式字典,查询__builtin__模块对象实质上是查询模块的locals()字典。
而本地的locals()字典经过了大量的查询速度优化,最好在locals()中查询。
函数加入命名空间的三种方式
1 | import timeit |
用dis模块分析
dis模块是对Python程序的字节码的分析,展现出函数等的调用次数。
1 | from dis import dis |
可以看出,LOAD_GLOBAL是查询了globals()字典,LOAD_FAST是查询了本地的locals()字典,LOAD_METHOD是对模块内方法的查询。
根据上述分析可以看出:
1、[模块].[方法]的调用方式用时最慢;
2、from [模块] import [方法]直接加载函数到命名空间,节省了搜索METHOD的时间;
3、保存函数引用,需要一次[模块].[方法]的查询,但为之后的调用节省了大量时间;
==然而,保存函数引用的方式并不是惯用写法,而在Python3.7中,经过时间分析,直接加载的引用方式更能节省查询时间。==
循环内查询的降速效果
1 | '''循环内查询的降速效果''' |
==千万级的循环中,循环内查询降速2.97%==
5、一些应用
5-1、计算元素个数
1、定义函数counter_dict,传入列表,计算列表中每个元素的出现次数。
1 | def counter_dict(items): |
2、使用collections.defoultdict生成字典,指定默认值。
P.S.使用
dict时,如果引用的Key不存在,就会抛出KeyError。如果希望key不存在时,返回一个默认值,就可以用defaultdict。需要注意的是,它作用于给字典赋值的时候,通过用户指定的函数,计算得到key的默认值。
1 | from collections import defaultdict |
3、使用collections的Counter类。
1 | from collections import Counter |
比较:
| Code | N=1000μs | N=2000μs | N=3000μs | 时间 |
|---|---|---|---|---|
| counter_dict(items) | 111.96 | 197.13 | 282.79 | O(N) |
| counter_defaultdict(items) | 120.90 | 238.27 | 359.60 | O(N) |
| Counter(items) | 51.48 | 96.63 | 140.26 | O(N) |
可以看出,效率排名为:Counter > dict > defaultdict
5-2、反向索引表
标签式搜索,需要进行预处理,好处大但代价高。
比如,遍历多个文章中的每一个单词,建立基于单词的反向索引表,就可通过查询单词找到含有该单词的文章。
注意,需要考虑到每一种可能的查询,或者灵活结合多种查询方法。
5-3、集合
6、总结
堆
字典树
迭代器与生成器
Numpy矩阵运算
编译为C
并发编程
并行编程
集群与工作队列
更少的RAM
Project
递归优化
以递归求解斐波那契数列第n项为例:
1 | from functools import lru_cache |