网络结构上的SIR模型模拟

Posted on Edited on In Views:
Symbols count in article: 9.2k Reading time ≈ 8 mins.
在网络结构上模拟SIR模型，并研究网络感染峰值。

网络结构上的SIR模型模拟

简介

网络无处不在。

自从1736年瑞士数学家欧拉（Leonhard Euler）孕育并使用图论解决了著名的哥尼斯堡七桥问题后，图论的发展就陷入了停滞，直到20世纪50年代，保罗·埃尔德什（Paul Erdos）发表对随机图研究，图论才被重新建立起来。

网络，其实就是图。

不论是万维网、社交网，还是蛋白质表达网络、蟋蟀心跳在无控制下的同步，其内在机理都与网络密切相关。

本篇在三个特殊的网络上模拟了传统的SIR模型，并探讨在不同的节点数量N下的感染峰值。

环境

R语言3.6.2 x64 + Rstudio

使用igraph和animation包，需要额外安装。

思路

graph TD
    A["设置参数及状态变量"] --> B["产生网络"]
    B --> C["初始化"]
    C --> D{"判断是否到达迭代终点"}
    D --"False"--> E["更新该时刻感染节点"]
    E --> F["取出到期的潜伏期节点，更新潜伏期节点序列"]
    F --> G{"判断取出的到期节点是否可以被治愈"}
    G --"True"--> H["治愈节点加入该时刻治愈节点序列"]
    H --> I["从该时刻感染节点中删去治愈节点"]
    I --> J["更新时刻"]
    G --"False"--> K["空节点加入该时刻治愈节点序列"]
    J --> D
    K --> I
    D --"True"--> L["打印GIF图"]
    L --> M("结束")

代码

让我们看看网络传染病在没有控制的情况下会怎样发展。

参数及状态变量设置

以下代码将设置模拟的基本参数，包括节点数量、潜伏期时间、感染率、治愈率（或死亡率）、模拟时间、状态初始值等。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
######################设置参数#######################
# 模拟节点数
N = 100
# 模拟时间单位
TIME = 70
# S、I、R初始数量
I = 1
R = 0
S = N - I - R
# 感染率
InfectedRate = 0.2586
# 治愈率（或死亡率）
RemovedRate = 0.0821
# 潜伏期时间
Time_Infected = 10
# 治愈期时间（预计用于带隔离项的模拟，此处暂未用到）
Time_Removed = 6
# 抛硬币概率：感染概率向量
Inf_porb = c(InfectedRate, 1-InfectedRate)
# 抛硬币概率：康复概率向量
Rem_prob = c(RemovedRate, 1-RemovedRate)

接下来我们设置在程序中记录节点状态的变量：

其实使用类来编程更为轻松和易懂，但是遗憾的是笔者并未深入学习R语言的这方面内容。就像MATLAB擅长于矩阵运算一样，R语言是为统计设计的语言。

1
2
3
4
5
6
7
8
9
10
11
#####################状态记录########################
# 记录总感染人数
TotalInfected = 1
# 治愈者随时间变化的列表
Removed_list = NULL
# 感染者随时间变化的列表
infected_list = NULL
# 用来为每个结点的潜伏期时间计数
TimeLine_Infected = NULL
# 用来为每个结点的治愈期时间计数（预计用于带隔离项的模拟，此处暂时未使用）
TimeLine_Removed = NULL

网络产生

产生指定网络：

  • 随机网络（Erdos-Renyi方法），自然界中几乎没有网络结构是随机的，因此随机网络更多是作为一个基准来研究其他结构化的网络。
  • 小世界网络（Watts-Strogatz算法），其熵值在规则网络和随机网络之间。小世界效应：随着少数随机链路加入有结构的网络上，其平均路径长度会快速减少。这个效应导致了“六度分隔”，即世界上的任意两个人能够通过约六个人建立联系。
  • 无标度网络（Barabasi-Albert方法）其度序列服从\(h(k)=k^{-q}\)的幂律分布。简单说来，就是少量高度节点(hub)和大量低度节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
library(igraph)
# 随机网络、小世界网络、无标度网络。

# Random Network(ER)：使用Erdos-Renyi方法生成随机网络，其生成方法有两个: G(n,p)和G(n,m)
g = erdos.renyi.game(N, 100, type = "gnm", loops = "TRUE")
# g = erdos.renyi.game(N, 0.03)
graph_name = "Random Network"

# Small World Network(WS)：使用Watts-Strogatz算法生成
# g = watts.strogatz.game(1, N, 3, 0.2)
# graph_name = "Small World Network"

# Scale-free Network(BA)：使用Barabasi-Albert方法生成
# g = barabasi.game(N)
# graph_name = "Scale-free network"

函数定义

定义一些函数：

  • 随机选择函数：用于对序列按照一定概率进行状态（S、I、R）的选择。
  • 更新感染者函数
  • 更新治愈者函数
  • 按时间序列绘图的函数：绘出从第1个时间单位到最后一个时间单位的图
  • 生成GIF图的函数

随机选择函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
####################随机选择函数########################
# 抛硬币决定该节点是否被感染
# 传入连接该节点的感染链接数，感染返回1，否则为0
# 最后加总每条链接的返回值，得出是否被感染
toss_Inf = function(freq) {
  tossing = NULL
  # 遍历每条链接
  for (i in 1:freq )
    # 按照指定概率向量随机取样，感染返回1，否则返回0
    tossing[i] = sample(c(1, 0), 1, rep=TRUE, prob=Inf_porb)
  # 加总所有链接的返回值，并返回
  tossing = sum(tossing)
  return (tossing)
}

toss_Rem = function(freq) {
  tossing = NULL
  for (i in 1:freq)
    tossing[i] = sample(c(1,0), 1, rep=TRUE, prob=Rem_prob)
  tossing = sum(tossing)
  return(tossing)
}

更新感染者函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#####################更新感染者函数#######################
# 更新感染后的节点，返回感染后全部受到感染的结点
update_infected = function(infected, total_time) {
  # 选取初始感染节点的领接节点
  nearest_neighbors = data.frame(table(unlist(neighborhood(g, 1, infected))))
  # 删去已感染的结点
  nearest_neighbors = subset(nearest_neighbors, !(nearest_neighbors[,1]%in%infected))
  # 删去已治愈的结点
  nearest_neighbors = subset(nearest_neighbors, !(nearest_neighbors[,1]%in%Removed_list[[total_time]]))
  # 返回更新的感染节点
  keep = unlist(lapply(nearest_neighbors[,2], toss_Inf))
  new_infected = as.numeric(as.character(nearest_neighbors[,1][keep >= 1]))
  # 去除重复的感染节点
  infected = unique(c(infected, V(g)[new_infected])) 
  return(infected)
}

更新治愈者函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
######################更新治愈者函数######################
# 更新治愈者
update_removed = function(wait_removed, day) {
  # 获得等待判断是否康复的结点
  wait_removed = data.frame(table(unlist(V(g)[wait_removed])))
  # 通过概率函数判断是否康复
  push = unlist(lapply(wait_removed[,2], toss_Rem))
  # 获得新康复结点
  new_removed = as.numeric(as.character(wait_removed[,1][push >= 1]))
  # 新康复者加入治愈者序列
  if (length(Removed_list[[day]]) == 0 && length(new_removed) == 0) {
    Removed_list[[day+1]] = V(g)[0]
  }else {
    Removed_list[[day+1]] = c(Removed_list[[day]], V(g)[new_removed])
  }
  return(Removed_list)
}

打印图片函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#################打印时间序列图片函数###################
plot_time_series = function(infected_list, Removed_list, total_time){
  # 获取每天感染的节点数
  num_inf = unlist(lapply(1:total_time, function(x) length(infected_list[[x]])))
  # 获取每天感染的比例
  p_inf = num_inf / N
  p = diff(c(0, p_inf))
  # 时间线
  time = 1:total_time
  plot(p_inf~time, type = "b", 
       ylab = "Inf", xlab = "Time",
       xlim = c(0,total_time), ylim =c(0,1))
  plot(p~time, type = "h", frame.plot = FALSE,
       ylab = "Dif", xlab = "Time",
       xlim = c(0,total_time), ylim =c(0,1))
}

####################打印动图函数########################
plot_gif = function(infected_list, Removed_list){
  d = 1
  while(d <= length(infected_list)){
    layout(matrix(c(1, 2, 1, 3), 2,2, byrow = TRUE), widths=c(3,1), heights=c(1, 1))
    # 设置不同状态的节点的颜色
    V(g)$color = "white"
    V(g)$color[V(g)%in%infected_list[[d]]] = "red"
    V(g)$color[V(g)%in%Removed_list[[d]]] = "yellow"
    plot(g, layout =layout.old, edge.arrow.size=0.2)
    title(paste(graph_name, 
                "\n Infected Rate =", InfectedRate,
                "\n Removed Rate =", RemovedRate,
                "\n Day", d))
    plot_time_series(infected_list, Removed_list, d)
    d = d + 1
    }
}

模拟开始

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#######################程序入口#########################
# 开始模拟
# 初始化，种子可另选
set.seed(138497)
# 等可能选取n个初始不同的结点
# 通过改变I的初始值能够设定初始有多少个感染者
infected = sample(V(g), I)
# 列表初始化，治愈者时间节点序列 & 潜伏期计数列表需要先赋值为空的网络节点，以便于做运算
infected_list = list()
TimeLine_Infected = list()
Removed_list = list()
Removed_list[[1]] = V(g)[0]
for (i in 1:Time_Infected) {
  TimeLine_Infected[[i]] = V(g)[0]
}
# 第1个时间单位的感染者序列和潜伏期时间
infected_list[[1]] = infected
TimeLine_Infected[[Time_Infected]] = infected
# 设置边和顶点的颜色
# 初始设置全部人群为易感人群，颜色为白色
# 之后能够设置感染者为红色，康复者为黄色
E(g)$color = "grey" # Edges
V(g)$color = "white" # Vertices
# 绘出初始状态图，设置绘图模式layout.fruchterman.reingold
set.seed(13413)
layout.old = layout.fruchterman.reingold(g, niter = 1000)
V(g)$color[V(g)%in%infected] = "red"
plot(g, layout =layout.old)
# 迭代
wait_removed = NULL
total_time = 1
while(total_time < TIME){
  infected_list[[total_time+1]] = update_infected(infected_list[[total_time]], total_time)
  # 取出等待判断是否治愈的结点，加入等待治愈的序列
  wait_removed = c(wait_removed, TimeLine_Infected[[1]])
  # 所有节点的计时器向前移动1，即下标-1
  for(i in 2:length(TimeLine_Infected)) {
    TimeLine_Infected[[i-1]] = TimeLine_Infected[[i]]
  }
  # 新增感染节点加入潜伏期计时序列
  TimeLine_Infected[[Time_Infected]] = subset(infected_list[[total_time+1]], !infected_list[[total_time+1]]%in%infected_list[[total_time]])
  # 新增治愈者加入治愈者时间序列
  if (length(wait_removed) != 0) {
    Removed_list = update_removed(wait_removed, total_time)
  }else {
    Removed_list[[total_time+1]] = Removed_list[[total_time]]
  }
  # 从当前时刻感染者序列中删去当前时刻的新增治愈者
  infected_list[[total_time+1]] = subset(infected_list[[total_time+1]], !infected_list[[total_time+1]]%in%Removed_list[[total_time+1]])
  # 从等待治愈的序列中删去已治愈的节点
  wait_removed = subset(wait_removed, !wait_removed%in%Removed_list[[total_time+1]])
  TotalInfected = length(infected_list[[total_time+1]])
  total_time = total_time + 1
}

library(animation)
# 保存GIF动图
saveGIF({
  ani.options("convert")
  plot_gif(infected_list, Removed_list)
}, ani.width = 800, ani.height = 500)

结论

我猜大部分读者会跳过代码部分，不过或许有一些初学者会希望自己重现这个过程，笔者也曾经是初学者，对于查找资料时看到的毫无注释和运行环境的代码十分头疼，所以还是给上述较为混乱的代码写了些注释。

这里需要说明，这个模拟是有很大局限的，现实世界中的许多影响因素不能很好地考虑进去。为方便理解和操作，这里说明影响结果的主要因素：

  • 种子(seed)：种子影响随机数生成过程，进而影响按概率选择、随机选择初始感染节点这两个过程。
  • 节点规模(N)
  • 状态转移概率(InfectedRate & RemovedRate)：影响节点易感、感染和治愈之间转移的概率。
  • 潜伏期时间(Time_Infected)
  • 模拟时间(TIME)
  • 网络生成参数

虽然已经说过这是在没有控制下的模拟，但是封路、口罩、消毒、医疗、政策影响、人自身主观能动性等因素可以通过“合理”调整状态转移概率和网络生成参数来达成。

至理名言：你的数学水平是永远也不够的。。。。。

要是笔者有更高的数学水平就不搞简单的模型了。。。

对于网络结构的说明

下面对于网络生成参数作简单的说明：

随机网络：

1
2
g = erdos.renyi.game(N, 100, type = "gnm", loops = "TRUE")
# g = erdos.renyi.game(N, 0.03)

有两种生成模式：gnm、gnp。首先确定节点数量n，之后可以以连接两个任意节点的概率p和总边数m来构造。

随机网络的平均度（平均每个结点连接了多少条边）为：\(avg\_degree=2m/n=np\)。

当节点数量非常大时，其度序列服从泊松分布。

小世界网络：

1
g = watts.strogatz.game(1, N, 3, 0.2)

第一个参数由于笔者还没搞懂所以就不解释了；第二个参数表示节点数量；第三个参数表示每个结点与多少个直接后继节点相邻；第四个参数表示重连概率，即前面三个参数构造好k-规则网络，再按第四个参数所规定的概率随机重连每条边。

无标度网络：

1
g = barabasi.game(N, power = 1)

用非数学的语言来描述，就是具有少量高度节点(Hub)（即连接到该节点的链路较多），大量低度节点的网络。

第一个参数表示节点数量；第二个参数表示偏好链接，其意义为：构造过程中，将新的节点连接到第i个节点的概率P为：\(P(i)=\frac{k_i}{\sum_jk_j}\)，\(k_i\)为第i个节点的连通性。（但是笔者没有查询到power是如何应用进去的）

简单的例子

我们以随机网络为例：

1
2
3
4
5
6
7
8
N=10; TIME = 50
I = 1; R = 0; S = N - I - R
InfectedRate = 0.2586
# 治愈率（或死亡率）
RemovedRate = 0.0821
# 潜伏期时间
Time_Infected = 7
g = erdos.renyi.game(N, 0.3)

通过设置连接概率为0.3，使得每个结点平均连接了\(Np=3\)个节点。

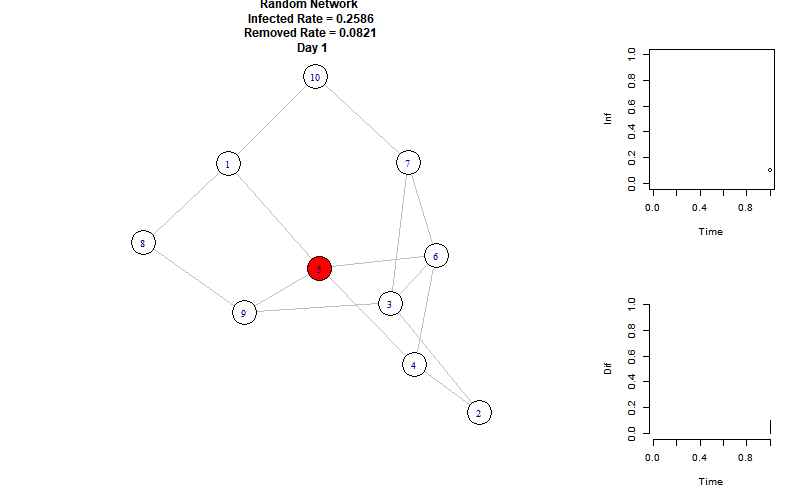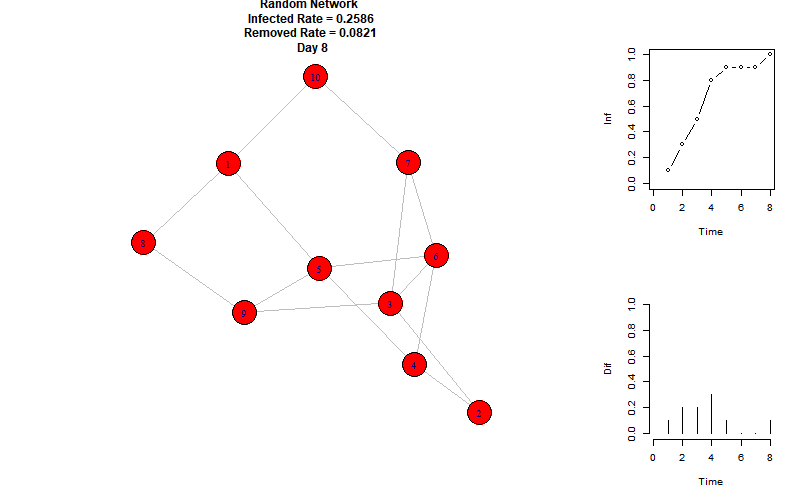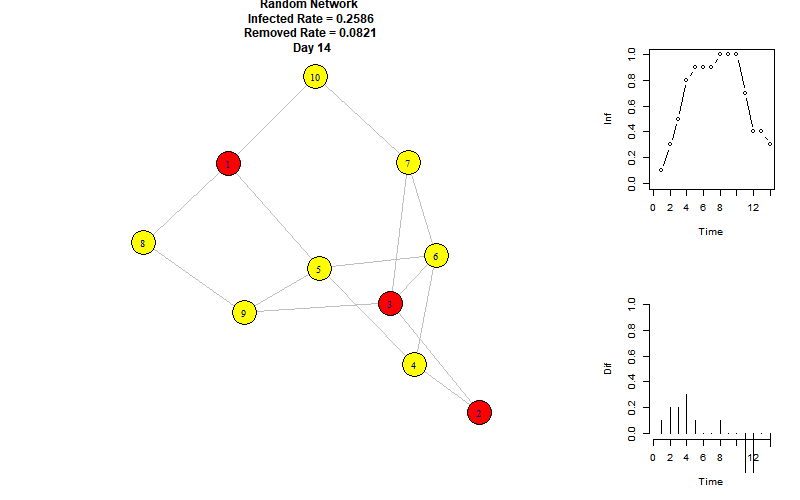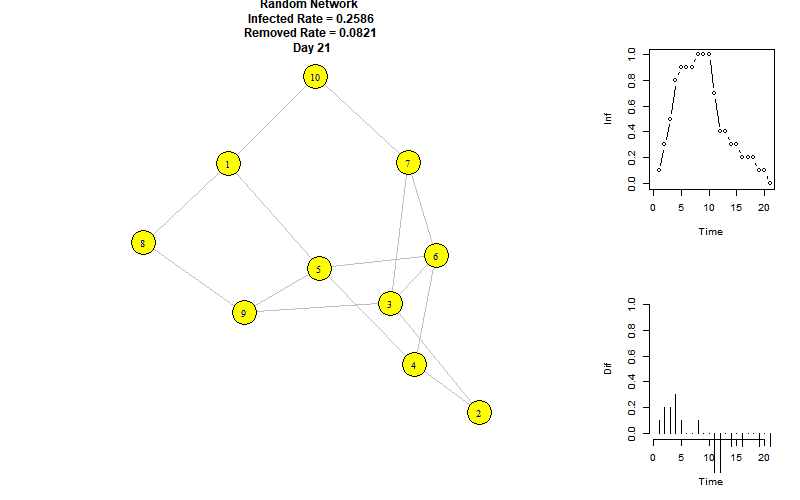
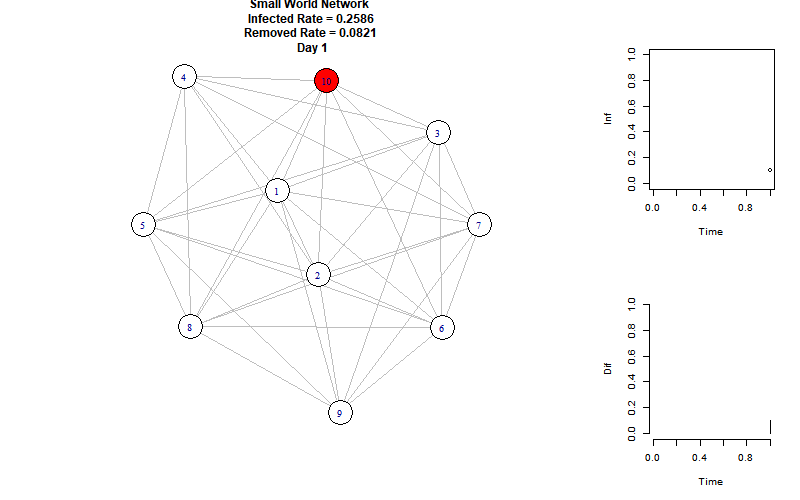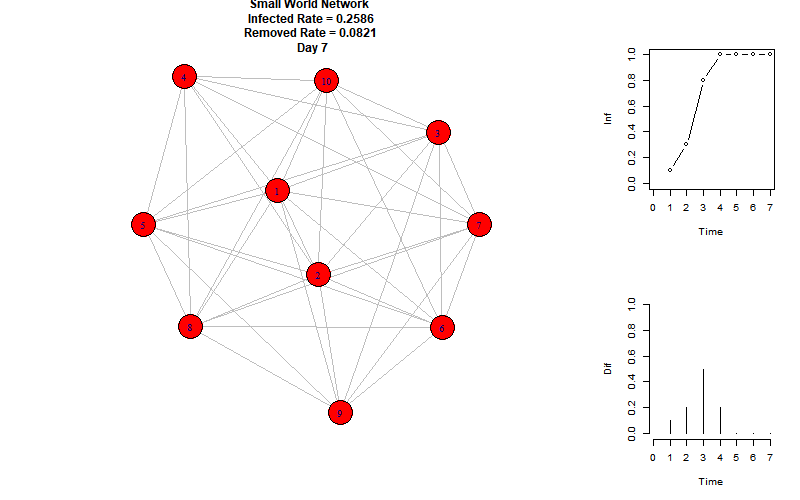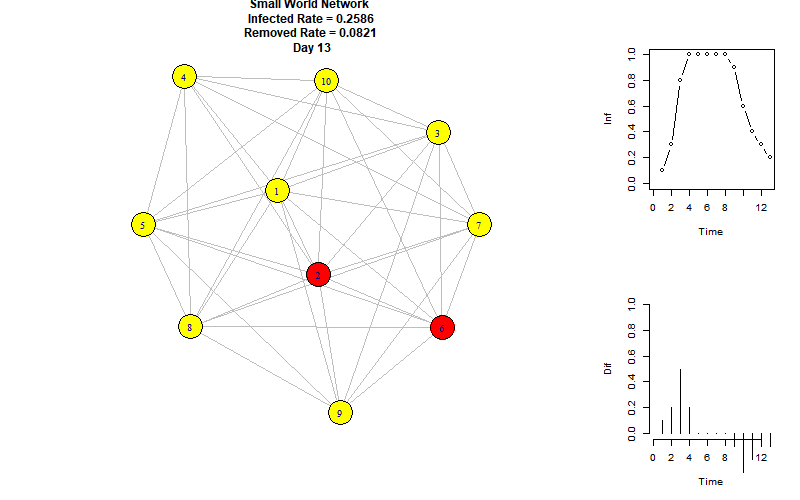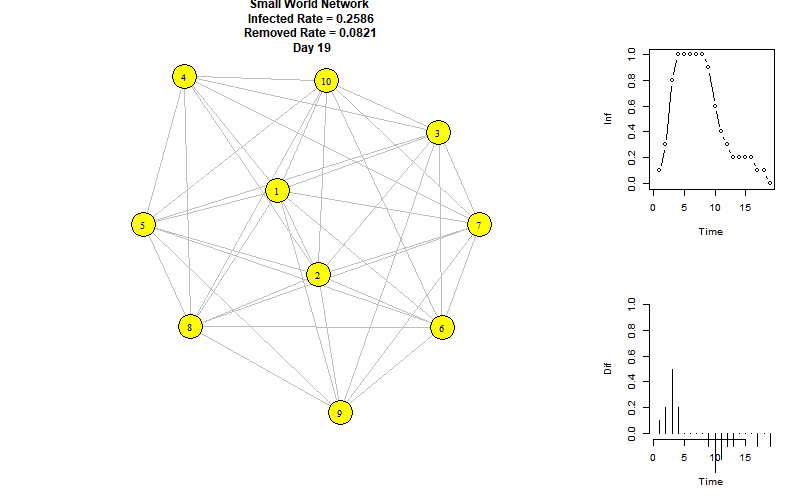
以下是模拟动图：

右上折线图表示每个时刻的感染节点比例，右下柱状图表示每个时刻增加的感染节点比例。

可以看到，当前参数下的感染峰值为100%，再第8个时间单位达到。

为啥不能聚餐拜年

让我们来看看疫情下的家庭聚餐。

假设你在一个大家庭里，亲戚往来平凡，过年总是有近20个男女老少聚在一起庆祝。你们聚餐时不戴口罩(。。。)，在一起玩了1天。

然而，有一位“潜伏者”在你们之中……

TIME表示时间单位，其单位并不一定是天(day)。

1
2
3
4
5
6
7
8
9
N = 20; TIME = 50
I = 1; R = 0; S = N - I - R
InfectedRate = 0.2586
# 治愈率（或死亡率）
RemovedRate = 0.0821
# 潜伏期时间
Time_Infected = 7
# 小世界网络，平均度为8
g = watts.strogatz.game(1, N, 4, 0.1)

可以看到，第4个时间单位，感染峰值就达到了100%。这个时间单位，可以代表2小时，可以代表1小时，也可以代表1分钟。。。

事实上，如果在空气流通较差的环境下，感染峰值出现的速度会更加快。

为啥进商场要戴口罩

话不多说，上图：

节点分布太密了。。。其实主要看右侧统计图就好

假设商场有2层，每层面积\(1500m^2\)，根据《全国民用建筑工程设计技术措施2009 规划·建筑·景观》视作地上3层（数字太大了笔记本承受不起。。。），所以商场共有2310人。使用平均度约为18的随机网络。

如果大家每天都去1个商场逛1-2小时，并且都不戴口罩，持续一个星期后，后果很严重。当然，模拟具有人流量和许多影响因素的商场误差还是很大的。

读者还可以自己模拟在不同的参数下，网络感染峰值会在怎样变化，从而得到防止疫情进一步发展的方向。

通过上述方法，我们还可以研究网络的平均度、谱半径等属性对于感染峰值的影响，这里就不在赘述了。

笔者又用代码水了一章，嘿嘿嘿。。。

参考文献

  1. 《网络科学：原理与应用》Ted G. Lewis著, 机械工业出版社, 2013年7月第1版
  2. 代码参考：http://www.sohu.com/a/144490909_8264345