神经网络学习_基本工作原理

前言

摘自Microsoft-ai-edu-B6-01.0

通常我们把三层以上的网络称为深度神经网络。两层的神经网络虽然强大，但可能只能完成二维空间上的一些拟合与分类的事情。如果对于图片、语音、文字序列这些复杂的事情，就需要更复杂的网络来理解和处理。第一个方式是增加每一层中神经元的数量，但这是线性的，不够有效。另外一个方式是增加层的数量，每一层都处理不同的事情。

1. 卷积神经网络 CNN (Convolutional Neural Networks)

对于图像类的机器学习问题，最有效的就是卷积神经网络。

2. 循环神经网络 RNN (Recurrent Neural Networks)

对于语言类的机器学习问题，最有效的就是循环神经网络。

神经元模型

神经网络由多个神经元分层连接在一起组成，神经元是最基本的构造：

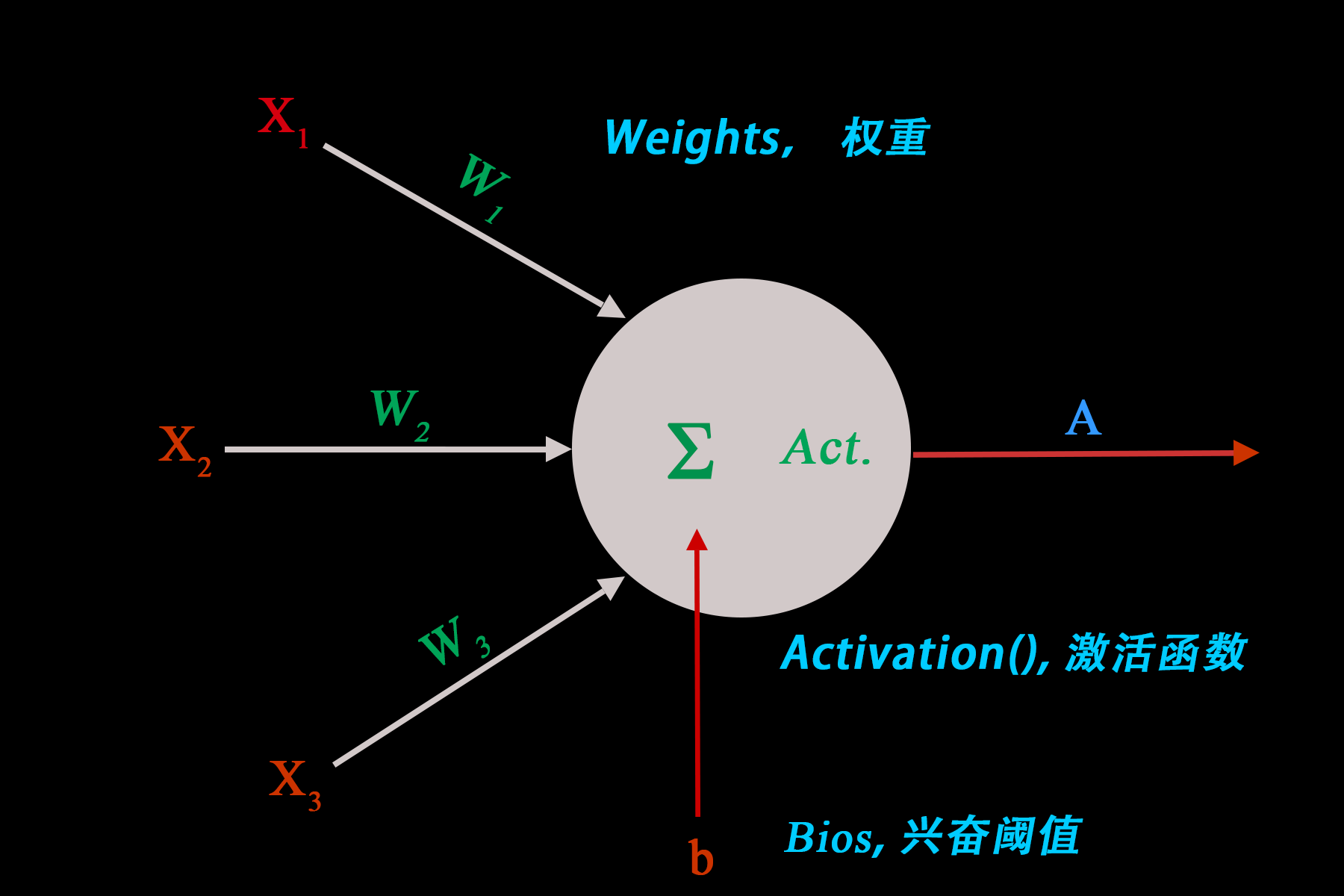
特性如下：

1. 多个输入\(X\)，单个输出\(A\)，单个兴奋阈值\(b\)（输出可连接多个神经单元）；
2. 初始权重\(W\)和兴奋阈值\(b\)有人为初始值；
3. 同一层神经元的激活函数必须一致；

过程描述

一个神经元接受多个输入信号\(X_1, X_2, X_3\)，并且每一条输入信号都有一个权重\(W_1, W_2, W_3\)，表示该输入对神经元的影响大小。

对于神经元来说，只有达到一定的兴奋水平才能够输出信号，因此需要有一个兴奋阈值\(b\)。

当\(X_1W_1+X_2W_2+X_3W_3\geq -b\)，也即\(Z=\sum_{i=1}^3XW+b\geq 0\)时，神经元输出信号。

当然，输出信号的大小根据\(Activation()\)激活函数计算，因此最终输出信号\(A=Activation(Z)\)。

激活函数

在这个神经元模型中未知的有初始权重、初始阈值和激活函数，前两者有初始值，并且需要被不断调整；而激活函数则需要人为选取。

为什么需要激活函数？

我们假设没有激活函数，那么我们看一个三层的简单神经网络：

这里要说一下神经网络的实质：用一个可以分类狗、猫、鱼的神经网络为例，我们将输入的动物图片变成二进制数据输入神经网络，它将输出字符“狗”、“猫”、“鱼”。这个神经网络在训练过程中实际上是建立了一个复杂的映射，将【狗的图片】映射为【“狗”】……，就像一个数学函数，将不同范围的自变量的值映射为因变量的值一样。

对于同一层的神经元，运用矩阵运算，可以写成\(Z=WX+B\)，其中\(W\)、\(X\)、\(B\)均为矩阵。

如果没有激活函数，则上一层的输出即为下一层的输入。

第一层：\(Z_1=W_1X_1+B_1\)

第二层：\(Z_2=W_2X_2+B_2\)，\(X_2=Z_1\)

第三层：\(Z_3=W_3X_3+B_3\)，\(X_3=Z_2\)

带入得到：\(Z_3=W_3[W_2(W_1X_1+B_1)+B_2]+B_3=W_3W_2W_1X_1+B_3W_3B_2+W_2B_1=WX_1+B\)

不管多少层，神经网络的输出还是输入的线性函数，其实质仍然是线性的。但是神经网络这个复杂的映射不大可能是简单的线性函数，因此需要用非线性的激活函数使得它能够学习复杂的映射。

理论上，两层神经网络能够无限逼近任意连续函数(Kolmogorov)。简单来说，一层用于空间变换，将非线性变为线性，另一层用于线性分类/拟合/回归。

另外，激活函数最好能够可导，因为后面需要我们通过其计算反向传播误差。

常见的激活函数有Sigmoid函数，图像如下：

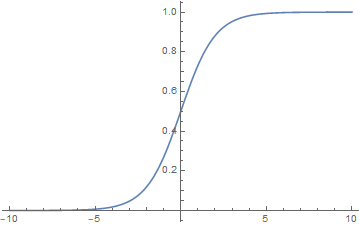
还有阶跃函数、双曲正切函数Tanh、ReLU函数等

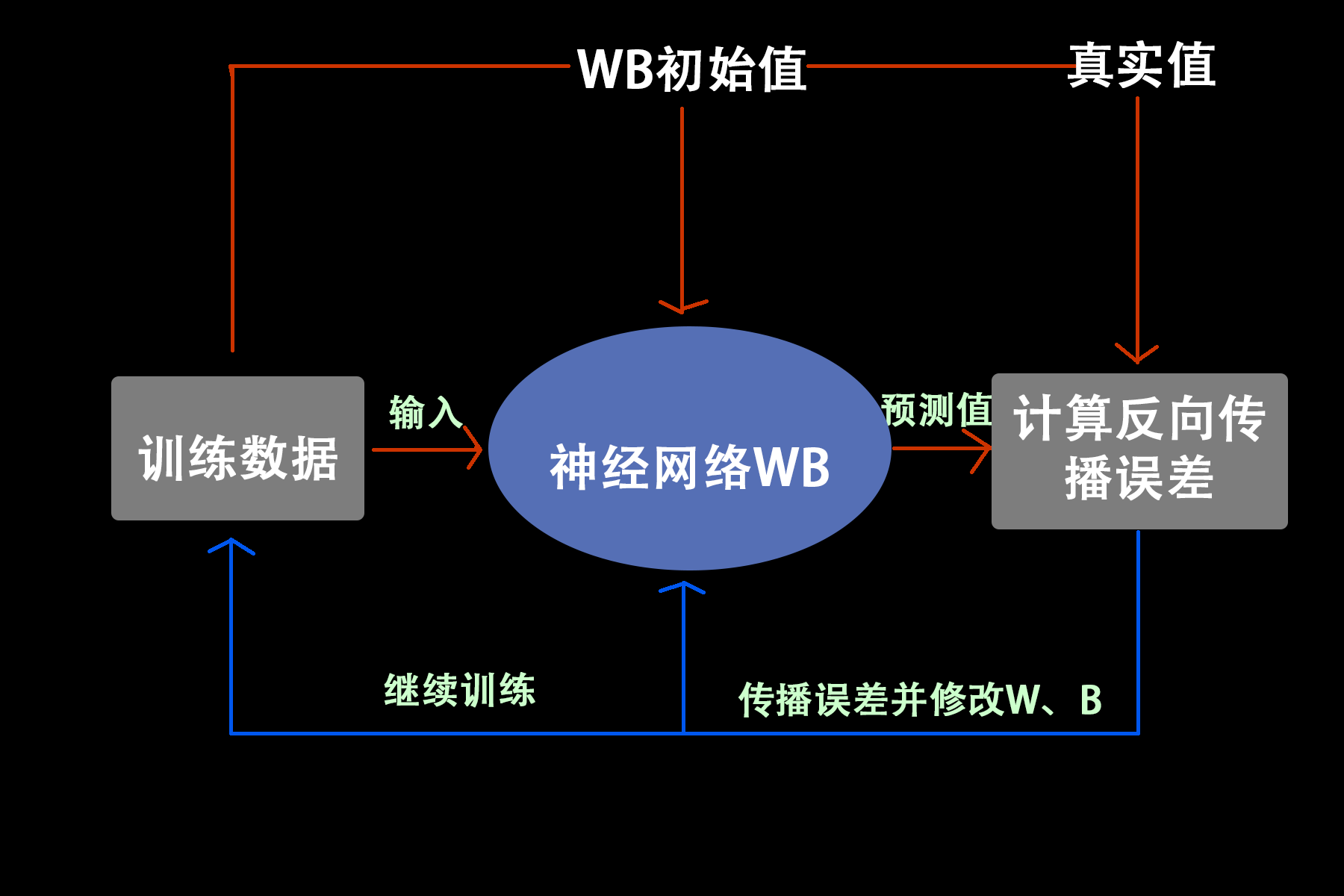
训练基本过程

1. 【训练数据】输入【神经网络W、B】，计算【预测值】
2. 【损失函数】计算【真实值】与【初始值】的【“差距”】
3. 【“差距”】传播回【神经网络W、B】，修改【权重矩阵W】【兴奋阈值B】
4. 返回步骤1，直到训练数据与轮数结束。

神经网络的主要功能

• 分类
• 回归/拟合

拟合	分类

图片来自Microsoft-ai-edu-B6-01.0

神经网络训练完成后，其权重组成一个函数参数的近似解。

我们来用橘子来说明：如果输入橘子图片，则输出1；否则输出0。这就是分类。如果输入橘子图片，程序输出0.8，这就是拟合，表示它是橘子的可能性用数字衡量为0.8。这就是拟合。