神经网络学习_反向传播与梯度下降（1）

Posted on Edited on In Views:
Symbols count in article: 4.7k Reading time ≈ 4 mins.
误差的反向传播与梯度下降，例子与简介。

神经网络学习_反向传播与梯度下降（1）

反向传播的简单例子

我们以一个简单的例子开头：

将 \(k,m,1\) 视作权重。

graph LR
    A[3]
    C[8]
    E[5]
    F[2]
    A -->|k| G["x=3k+8m"]
    C -->|m| G
    E -->|m| H["y=5m+2"]
    F -->|1| H
    G --> I["z=xy"]
    H --> I

Calc_1

当 \(k_0=1, m_0=3\) 时，\(z_0=459\)。

如果想使得 \(z_1=450\)，分别只考虑 \(k,m\)，它们的值分别该如何变化？

很自然的想法就是在 \(z=xy=f(k,m)\) 上研究其增减性。

只考虑 \(k\)，则：

\[ z=xy=f(k,m_0),\;\frac{\partial{z}}{\partial{k}}=\frac{\partial{z}}{\partial{x}}\frac{\partial{x}}{\partial{k}}=3y \] 那么在 \(k_0=1,m_0=3\) 附近，函数 \(f(k,m_0)\) 关于 \(k\) 的导数为： \[ \frac{\partial{z}}{\partial{k}}|_{k=1,m=3}=51 \] 根据上式可以有如下计算：

\(\therefore\lim\limits_{\Delta k\to 0}\frac{\Delta z}{\Delta k}=51\)，即 \((\Delta k\to 0)\Delta z=51\Delta k\)；

\(\because\Delta k=(z_1-z_0)/51\approx -0.1765=k_1-k_0\)；

\(\therefore k_1=0.8235,x=3k_1+8m_0=26.4705,z=xy=449.9985\)。

emmmm，好像选的值比较好，第一次计算就达到了比较好的精度，但是很多情况下，是无法一次达到的。因为我们使用的导数是在原来点附近的极小范围内起作用。

Calc_2

如果同时改变 \(k,m\) 呢？

  1. 不妨设 \(W_k=0.5,W_m=0.5\)，即二者对于结果影响的权重分别为 0.5，0.5；
  2. 计算 \(\frac{\partial{z}}{\partial{k}},\frac{\partial{z}}{\partial{m}}\)；
  3. 则 \(\Delta k=\Delta zW_k/\frac{\partial{z}}{\partial{k}}\)，\(\Delta m=\Delta zW_m/\frac{\partial{z}}{\partial{m}}\)；
  4. 更新 \(k,m\)：\(k=k+\Delta k,m=m+\Delta m\)（这里的 \(\Delta\) 指新的值减去旧的值）；
  5. 计算 \(z\) 和目标值之间的误差，若超过误差范围，则返回步骤2。

如果函数是非线性的，同样使用偏导数计算，将误差一层一层反向传递。

反向传播与梯度下降

通俗地讲，神经网络的训练过程就是根据自己原有的方法，先预测一个值，然后拿到真实值进行比较。它一看，欸，我跟真实值的误差有这么多，然后就根据这个误差，运用梯度下降的原理，调整自己的计算方法，再进行计算。

这跟猜数字的游戏很像，你报一个数，我猜一个数，你告诉我差距怎样，我对猜数的方法进行调整……

梯度下降法

基本思想

就跟下山一样，选择“视野”内最“陡”的一条路下山。

它是求解非线性规划问题的一种方法，用于求可微函数\(f(X)\)的最值（极值）。

我们的目标是使得通过误差函数计算出来的误差值最小。

我们的基本思想是：

  • 选择初始值 \(X^{(0)}\)
  • 依照某种规则选择”更好的“ \(X^{(k)}\)，使得 \(f(X^{(k)})<f(X^{(0)})\)
  • 得到解序列 \(\{X^{(k)}\}:\lim\limits_{k\to +\infty}\|X^{(k)}-X^{*}\|=0\;(X^*为f(x)最（极）小值)\)

所以，根据函数在该点的负梯度方向是该点的函数值下降最快的方向，我们可以采用如下规则选择更好的\(X\)： \[ X^{(k+1)}=X^{(k)}-\lambda\nabla{f(X^{(k)})} \]

当神经网络的输出变成上述的 \(X^{(k+1)}\) 时，选取合适的步长 \(\lambda\)，就能够使损失函数值 \(f(X^{(k+1)})<f(X^{k})\)（损失函数的选取一般使得 \(f(X)\) 非负），也就是与标签值差距更小了。

这样，我们就可以根据目标输出 \(X^{(k+1)}\) 去反向计算，调整各层的权重了。

这里的\(X\)是向量，在训练中是指神经网络输出的预测值。

样本空间

  • Data Set
  • Document \(\to\) Instance / Sample
    • Attribute / Feature \(\to\) Attribute Value。
  • Attribute Space / Sample Space
  • Feature Vector

简单说来，属性空间内各个维度代表不同的属性，而每一个样本都由一组特定的属性值组成，成为属性空间内的一个点。

e.g. 假定油菜籽能用含油量、品种两个属性描述，我们需要把它们分为好榨油的油菜籽和不好榨油的油菜籽，那么一个样本就可以用一个向量表示：

\(\lambda\)如何确定

还有一个问题是，\(\lambda\)该如何确定？

\(\lambda\)决定了每次往最速下降方向走多少距离，这是个问题，不恰当的话可能会震荡：

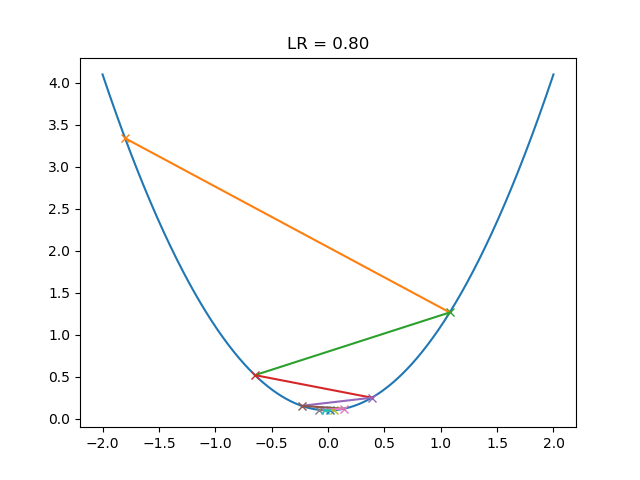
或者在两个取值间反复横跳，无法下降：

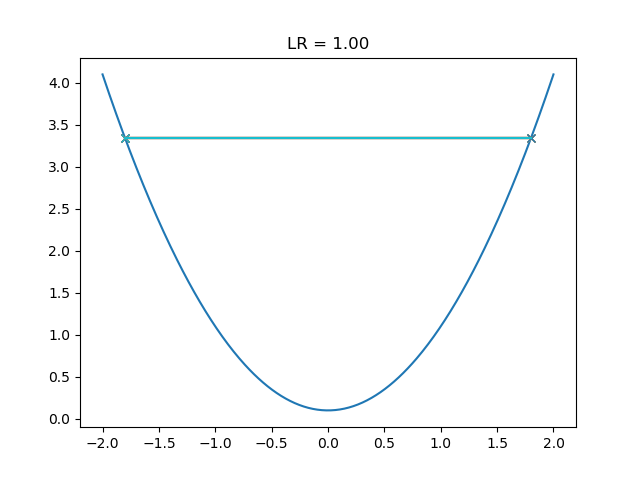
这一个学习率在极值点附近会产生震荡：

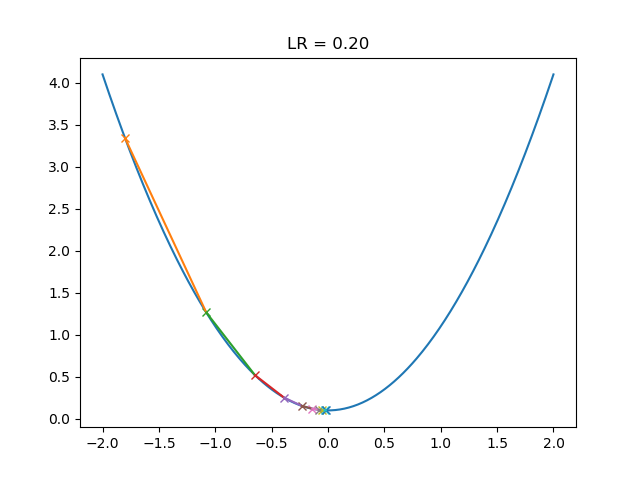
这个看起来很合适，就是需要更多的迭代：

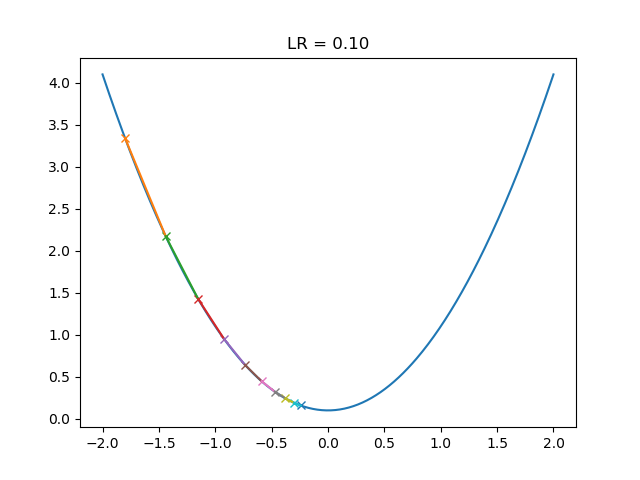
其实这里的步长\(\lambda\)就是接下来的学习率，学习率并不是越高越好。

如果设定过高，数学上来讲梯度下降算法可能难以收敛，发生梯度爆炸；过小则容易被困在“更差”的局部最小值里，收敛很慢。

“...较高的学习速率... 表示系统含有太多的动能，参数向量在处于混沌状态下，不断来回反弹，无法稳定到损失函数的一个较深且较窄的最优值”cs231n

我们可以通过代码模拟一下：见文末附录

Python构造神经网络_1

经过这两篇的说明，我们可以尝试使用python自己写一个超简单的三层神经网络（输入层、隐藏层、输出层）。

笔者不会TensorFlow、PyTorch、Keras、PaddlePaddle等框架，但是基于可持续发展的理念，选择深入学习内在机理。这里分享一下自己的学习经历。

准备

Python环境：Windows， Python3.7， IDLE

依赖：numpy, scipy, matplotlib, csv使用pip安装

说明

根据第一节内容可以知道：

  • 我们需要有三层，每层若干个神经元结点。
  • 第一层称作输入层，用于接收输入的数据；第二层称为隐藏层，用于抽象化输入数据的特征，以便更好线性分类；第三层称为输出层，输出判断结果。
  • 每个结点都需要经过激活函数再输出。
  • 上一层的输出作为下一层的输入。
  • 相邻两层之间，存在权重矩阵。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#!\usr\bin\env python3
#-*- encoding: utf-8 -*-
__author__: 'QCF'

import csv
import numpy as np
import scipy.special
import matplotlib.pyplot as plt

# 定义神经网络类
class neuralNetwork:

    # 初始化神经网络
    def __init__(self, InputNodes, HiddenNodes, OutputNodes, LearningRate):
        # 设置输入层、隐藏层、输出层感知机数量
        self.in_nodes = InputNodes
        self.hid_nodes = HiddenNodes
        self.out_nodes = OutputNodes
        # 学习率
        self.LR = LearningRate
        # 权重矩阵W_ih, W_ho表示Input到Hidden，Hidden到Output的权重矩阵
        # 形式如下：
        # w_11 w_12
        # w_21 w_22
        # w_ij表示上一层第i结点到下一层第j结点的权重值
        self.W_ih = np.random.normal(0.0, pow(self.hid_nodes, -0.5), (self.in_nodes, self.hid_nodes))
        self.W_ho = np.random.normal(0.0, pow(self.out_nodes, -0.5), (self.hid_nodes, self.out_nodes))

        # 激活函数为sigmoid函数
        self.activate_func = lambda x:scipy.special.expit(x)
        self.inv_activate_func = lambda x: scipy.special.logit(x)

这里有几个问题：

  1. 为什么权重矩阵要用参数为如下所示的正态分布： \[ \begin{align} &\mu=0\\ &\sigma_1^2=1/\sqrt{self.hid\_nodes}\\ &\sigma_2^2=1/\sqrt{self.out\_nodes} \end{align} \] 来初始化，而不采用通常的标准正态分布，或者是全为0呢？

  2. 输出层的神经元个数如何确定？

小小的总结

至此，我们大致了解了一下神经网络的基本原理以及梯度下降法。限于篇幅，损失函数以及如何计算反向传播误差将在下篇说明，并且将附上矩阵运算的说明。

附录

梯度下降模拟代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#!usr/bin/env python3
#-*- encoding: utf-8 -*-
__author__ = "QCF"

import numpy as np
import matplotlib.pyplot as plt

# 目标函数
def Fun(x):
    y = pow(x, 2) + 0.1
    return y

# 目标函数的导数
def dFun(x):
    y = 2*x
    return y

# 模拟不同学习率LR下的梯度下降，迭代10次
def Generate_d(LR):
    # 初始点x，P储存每次得到的新点坐标
    x = -1.8
    P = [[0,0] for i in range(10)]
    for i in range(10):
        P[i][0] = x
        P[i][1] = Fun(x)
        dx = dFun(x)
        x = x - LR * dx
    return P

# 绘出函数
def Draw_Fun(LR):
    x = np.linspace(-2, 2, num = 400)
    y = Fun(x)
    plt.plot(x, y, '-')
    P = Generate_d(LR)
    for i in range(10):
        plt.plot(P[i][0], P[i][1], 'x')
    for i in range(9):
        plt.plot([P[i][0], P[i+1][0]], [P[i][1], P[i+1][1]], '-')
    plt.title("LR = {:.2f}".format(LR))
    plt.show()

if __name__ == "__main__":
    LR = [1.0, 0.8, 0.6, 0.4, 0.2, 0.1]
    for r in LR:
        Draw_Fun(r)