数据库原理与应用_关系数据库

关系的形式化定义

域（Domain）：\(D\)

笛卡尔积（Cartesian Product）： \[ D_1\times D_2\times\cdots\times D_n=\{(d_1,\;d_2,\;\cdots,\;d_n)\;|d_i\in D_i,\;i=1,2,\cdots,n\} \] 基数（cardinal number）：一个域允许的不同取值个数。

关系（Relation）：笛卡尔积的子集。\(R(D_1,D_2,\cdots,D_n)\)

• 候选码（candidate key）：能唯一标识一个元组的最小属性集合。
• 主码（Primary Key）：若有多个候选码，则取其一为主码。

例如，\(学生(ID，身份证号，姓名，年龄)\)，则：

1. 候选码为 \(\{ID，身份证号\}\)；
2. 主码为 \(ID\) 或 \(身份证号\)。

• 主属性（primary attribute）：候选码的各个属性。
• 非主属性（non-primary attribute）：非候选码的各个属性。

又如，\(学生选课(SID,\;SName,\;CID,\;CName)\)，则：

1. 候选码为 \(\{\;(SID,\;CID)\;\}\)；
2. 主码为 \((SID,\;CID)\)；
3. 主属性为 \(\{\;SID,\;CID\;\}\)；
4. 非主属性为 \(\{\;SName,\;CName\;\}\)。

全部属性都是候选码，称为 全码（all-key）。

关系模式（relation schema）：\(R(U,\;D,\;DOM,\;F)\)。即：关系名 R、属性集合 U、属性的域 D、属性向域的映像集合 DOM，属性间数据的依赖关系集合 F。

关系的完整性

• 实体完整性
• 参照完整性
• 用户定义的完整性

实体完整性

实例（元组）可以唯一区分。即主属性不可取空值。

参照完整性

实体与实体之间的联系 \(\to\) 关系

关系与关系之间的联系 \(\to\) 属性的引用

\(Student(\underline{ID},\;Name,\;Age)\)

\(Course(\underline{CID},\;CName)\)

\(TakeCourses(\underline{SID,\;CID},\;Grade)\)

关系 \(TakeCourse\) 通过 \(Student\) 和 \(Course\) 的 PK 联系起来。

也就是说 \(TakeCourse\) 中 \(SID,\;CID\) 的取值需要 参照 另两个关系中的对应属性。

外码（Foreign Key, FK）：关系 \(R\) 的一个或一组非码属性 \(F\) 与 关系 \(S\) 的主码 \(K_S\) 相对应，则称 \(F\) 是关系 \(R\) 的外码，\(R\) 是参照关系，\(S\) 是被参照关系。

允许 \(R=S\)

简单说来就是一个关系的非码属性参照了另一个关系的主码取值，产生了联系。

• 参照关系 \(R\) 中，外码的取值：
  • 空值 NULL
  • 被参照关系 \(S\) 的主码值

用户定义的完整性

用户定义的约束条件。

关系代数

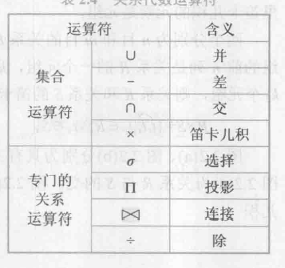
广义笛卡尔积：\(R\times X=\{\overset{\frown}{t_rt_s}|t_r\in R\land t_s\in S\}\)

\(\overset{\frown}{t_rt_s}\) 为元组的连接。

• \(t[A_i]\)：元组 \(t\) 中相应于属性 \(A_i\) 的一个分量

• 给定关系 \(R(X,Z)\)，\(X,Z\) 为属性组。当 \(t[X]=x\) 时，\(x\) 在 \(R\) 中的象集定义为： \[ Z_x=\{t[Z]\;|t\in R,\;t[X]=x\} \]